Metoda stosunków odległości
Z poprzedniej metody już wiemy jak określić czy przeciwnik jest np. wyżej. Dobrze, ale teraz jeżeli chcemy wywołać np. atak pod kątem 45o, to nawet kiedy przeciwnik będzie bardzo blisko i jednocześnie bardzo wysoko, to postać nie trafi. W takiej sytuacji trzeba wziąć pod uwagę nie tylko oś Y ale też X. W sytuacji kiedy przykładowo dystans to 100 pikseli na obu osiach mamy do czynienia z kątem 45o, czyli ze stosunkiem jeden do jednego. Wystarczy podzielić przez siebie P2Dist, uznałem że najlepiej będzie wstawić oś Y w mianowniku bo kiedy postać będzie na równi z przeciwnikiem P2Dist Y = 0. Oczywiście P2Dist X też może być równy 0 ale to w 2 sytuacjach, kiedy przeciwnik jest nad lub pod postacią, oczywiście Mugen zasygnalizuje błąd dzielenia przez 0 ale nie wyłączy się. Można dla pewności stosować dodatkowe funkcje albo założenia nie doprowadzające do wykonania dzielenia przez 0.
P2Dist Y / P2Dist X = 1 ; Kiedy dystanse są równe np. 100/100 = 1/1 = jeden do jednego = 1.
Oczywiście ciężko jest natrafić na taki stosunek, więc jak w poprzedniej metodzie musimy stworzyć zakres odpowiednich wartości. Sprawdzać można gotowy stosunek wielkości np. (1/2), (3/1), lub wartość liczbową wynikającą z tego stosunku np. 0.5, 3, itd.
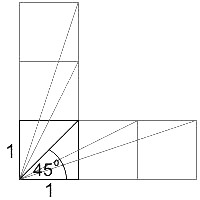
Jak widać metoda ta nie jest zbyt dokładna i posługiwać można się nią na wyczucie. Patrząc na rysunek łatwo stwierdzić, że dążąc do kąta 0o stosunek odległości dąży do 0, podobnie dążąc do kąta 90o stosunek dąży do nieskończoności. Bez zagłębiania się zbędnie w zawiłości obliczania kątów w takiej sytuacji, można patrzeć na rysunek i rozważyć wartości stosunków też w inny sposób. Można przyjąć, że przy kącie 45o mamy do czynienia ze stosunkiem równym 1. Co za tym idzie od kąta 0o do 45o mamy liczby od 0 do 1, czyli dla liczby o połowę mniejszej równej 0.5 mamy kąt 22.5o. Od kąta 45o do 90o mamy liczby od 1 do nieskończoności, więc tak samo dla liczby dwukrotnie większej równej 2 mamy kąt 67.5o. Jak już wspomniałem wszystko to nie oznacza oczywiście że dla liczby 4 kąt będzie wynosił 112.5o a wręcz przeciwnie nadal nie osiągnie 90o, wystarczy zerknąć na rysunek. Kąt będzie wzrastał o miarę wprost proporcjonalnie mniejszą do wzrostu stosunków odległości i podobnie w drugą stronę. Czyli przy stosunku odległości równym 2, kąt wzrośnie o 22.5o czyli będzie 67.5o, ale przy stosunku równym 3 wzrośnie dodatkowo o 11.25o co da 78.75o. Oczywiście kąty te podane są w ogromnym przybliżeniu bo nie można od tak przełożyć kąta na liczbę.
Przykład:
[State 1, w gore 90] trigger1 = p2dist Y / p2dist X < -2 type = varset v = 1 value = 4 [State 1, w gore 45] trigger1 = p2dist Y / p2dist X = [-2, -0.5) type = varset v = 1 value = 2 [State 1, na rowni] trigger1 = p2dist Y / p2dist X = [-0.5, 0.5] type = varset v = 1 value = 1 [State 1, w dol 45] trigger1 = p2dist Y / p2dist X = (0.5, 2] type = varset v = 1 value = 3 [State 1, w dol 90] trigger1 = p2dist Y / p2dist X > 2 type = varset v = 1 value = 5

 Infinity MUGEN
Infinity MUGEN
